| Main | Contact | Math |
Funny Functions talk
Thanks to everyone from UConn who came to my talk on 10/26/05!
Abstract:
Can a function in one real variable be discontinuous at every rational
number but continuous at every irrational number? Such a function not
only exists, but we can write down an explicit formula and graph it with a
computer.
The main emphasis will be on
cool pictures of this and other bizarre functions. I will
discuss examples of functions with oddly behaved derivatives as well as fractal
functions.
References:
- Gelbaum, Olmsted, "Counterexamples in Analysis"
- H. Whitney, "A Function Not Constant On A Connected Set of Critical Points" Duke Math. J. 1 (1935), 514-517
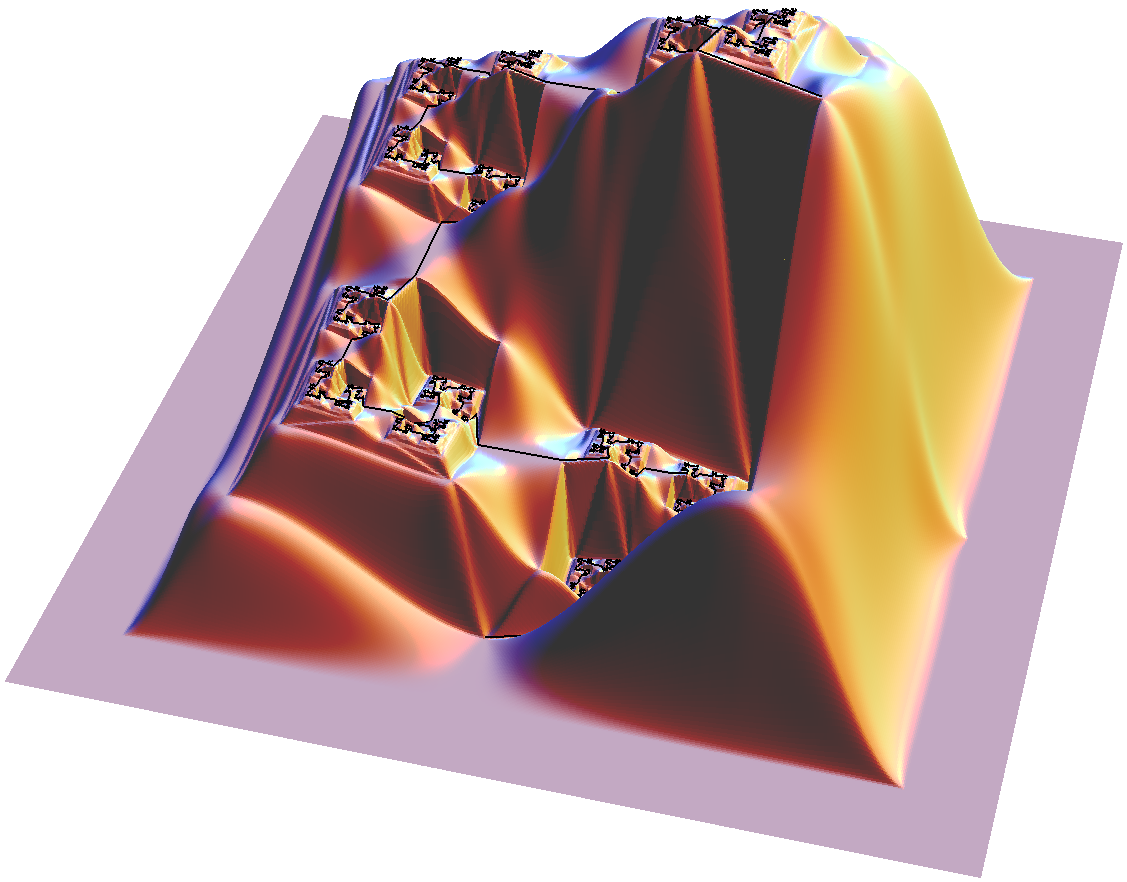
In Whitney's paper, he mathematically constructs a trail that winds its way up a mountain. Astonishingly, the mountain is flat (has a horizontal tangent plane) at each point of the trail, yet the trail still manages to ascend.
Whitney explicitly constructs the trail in his paper, but he only proves the existence of the mountain; he never explicitly constructs it. One highlight of this talk is an outline of my own explicit construction of the mountain.
Image of Whitney's mountain: